Dynamic Early Warning and Action Model: A policy evaluation tool

Introduction

The last decade has seen an explosion in the capabilities of quantitative forecast methods for armed conflict prediction. These are currently widely deployed for analytical purposes. However, their use for prevention poses challenges as policy options are typically not evaluated in systems that integrate quantitative forecasts.¹

The Dynamic Early Warning and Action Model (DEWAM) is an attempt to fill this gap. It combines two modules:

• Uses machine learning and text data to generate accurate forecasts of outbreak (risk of armed conflict) and intensity (no. of fatalities).²
• Targeted detection of ‘hard-to-predict’ onsets i.e. outbreaks of conflict in countries with a long history of peace.

• Integrates the forecasts to support decision-making.
• Allows for the simulation of specific policies and policy combinations.
• Quantitatively estimates returns to policies to facilitate internal debate at strategic and operational levels.

The key trade-off that policymakers face in prevention is that, first, acting on low risks means that resources are wasted on crises that never materialise but that, second, waiting for crises to materialise means that countries get stuck and suffer negative dynamics (conflict trap).

This document uses Nigeria as a case-study to describe the DEWAM. We then provide updated policy gains from our model for 160+ countries under a range of assumptions in theUpdated Prevention Gainssections.

¹ See the taxonomy provided by FP21 in the appendix, Figure 11.

² National (170+ countries) and subnational (60,000+ grid cells) conflict predictions are updated monthly and are freely available at https://conflictforecast.org/. Note that the armed conflict (outbreak) prediction is the likelihood of future armed conflict. However, for countries already in conflict, this is less informative. The intensity forecast predicts the number of fatalities which can provide insight into the potential for escalation/de-escalation.

Methodology

1. Forecasting module

As a primer, this module uses machine learning methods. These are statistical techniques that identify patterns and trends in historical data to produce estimates about what might happen in the future. These methods are extremely flexible and have come to dominate forecasting. But, they require a lot of data to learn due to this flexibility.

For conflict prediction, naive approaches use historical violence as a proxy for future violence. However, predicting a continuation of conflict for countries currently in conflict, or a continuation of peace for countries currently at peace, is of limited benefit to policymakers. The most useful, and most difficult, cases to identify are where the country has a long history of peace but is suddenly becoming susceptible to violence. These cases are rare. Therefore, it is necessary to go far back in time to provide the machine learning algorithm with sufficient instances of outbreaks to learn from.

This is the key innovation of our forecasting model - the use of news text data reaching back to the 1980s to capture outbreaks in these hard-to-predict cases. Over 5 million newspaper articles are geo-located and broken down into a set of 15 distinct topics.³ We find:

• Text is particularly powerful for capturing increasing risk in countries with a long history of peace.
• Topics such as “military conflict” or “judicial abuses” are positively associated with risk, i.e. with more news stories on police violence or the movement of guerilla groups, the risk increases.
• Other topics such as “power and negotiation” or “economics” are negatively associated with risk. When their share in reporting falls, a country is more likely to be at risk.

³ See examples of text topics and topic-specific vocabulary in the appendix, Figures 12 and 13.

Methodology

2. Dynamic decision-making module

This module provides a framework that enables the forecast to support policy-makers in a practical way. We seek to answer key questions such as:

• At which countries should attention and resources be targeted?
• At what point should a country office escalate risk warnings to attract attention?
• How does a strategic view on policies change the optimal decisions taken?
• Should the focus be on prevention, de-escalation or a combination of the two?
• How can policy-makers combine policies most effectively to build pathways out of violence?

In order to effectively answer these questions we introduce a model that is built on top of the forecasting module.

Figure 1: Building blocks of the dynamic decision-making module

The foundation of the dynamic decision-making module is what we call risk stages.

Building block 1: Risk stages

By examining the dynamics of conflict in the past, we distil the cycle of peace and conflict into a spectrum of 12 stages.⁴ In this way, every country is assigned to a stage for every month.⁵ It is easiest to think of stages as summaries of conflict situations. In general, the higher the stage, the more severe the situation. Figure 2 reports a simple characterization of the stages. We report the mean values, conditional on the observed stage, for the forecasts from module 1 and the intensity of violence.

Figure 2: Descriptive summary of risk stages

• Stages 1-4, stable peace: In these stages we expect no fatalities resulting from conflict and a low risk of future conflict. For example, Iceland and Switzerland have spent the entire time-span in stage 1.
• Stages 5-10, elevated risk: These stages generally capture countries that are on the precipice of conflict or have recently experienced violence and are susceptible to recurrence. We expect low levels of deaths in these stages, but increased risk of an outbreak. For example, in the two months directly before the invasion of Crimea, Ukraine was in stage 6 and 8.
• Stages 11 and 12, intense conflict: These stages represent ongoing violence, but are differentiated by its intensity. On average, a country experiences 6 deaths per 1mn inhabitants when in stage 11, compared to 84 deaths per 1mn when in stage 12. Nigeria and Mexico have spent extended periods in stage 11, whilst Afghanistan, Syria and Central African Republic have suffered the most from being in stage 12.

Figure 3 illustrates these stages using the stage history for Nigeria and a selection of comparable countries.

Figure 3: Stage visit comparison, Jan 2010 to April 2023

⁴ The stages are generated using a statistical method (Hidden Markov Model) using the forecast as the primary input. The number of stages is determined via experimentation.

⁵ The latest model is trained on data from January 2010 to April 2023.

Building block 2: Conflict dynamics

The next step is to model conflict dynamics via a transition matrix.⁶ It represents the likelihood that a country moves from one stage (the row) to any other (the column) within the next three months. This is the engine of our modelling approach since it permits going beyond static representations of the world to dynamic ones.

Figure 4: Transition matrix

Figure 4 shows this transition matrix visually. The darker the shade of red, the higher the probability of this transition. We see that:

• Stages are sticky: Notice the deep, dark red hue across the diagonal of the matrix. Stages are most likely to transition to the same or similar stage. For example, the likelihood of starting in stage 1 and ending up in stage 1 three months later is over 93%.
• Peace is stable: Notice the light orange area in the top right corner. This shows it is rare for countries to start in stages 1, 2, 3 or 4 and transition to stage 11 or 12. Instead, countries usually pass from stable peace into a period of elevated risk, rather than directly to violence. For example, imagine you are in stage 4. The likelihood of moving to any of stages 5-10 is 9%, whilst the likelihood of moving to any of stages 11-12 is 0.2%.
• The conflict trap: Similarly, countries rarely transition from stage 11 or 12 to stage 4 or lower - the light orange area in the bottom-left corner. In order to escape conflict, they generally experience extended periods of elevated risk before settling into a peaceful stage.

⁶ The transition matrix is derived from the stage transitions for all countries for the period January 2010 to April 2023.

Building block 3: Conflict damages

So far we have summarised the historical dynamics of conflict via risk stages and a transition matrix. The essence of this element is to capture how the risk stages are associated with measurable outcomes.⁷ We focus on the relation between stages and GDP growth, fatalities, displacement, and overseas development assistance (ODA).⁸

First consider a static view of the world as shown in Figure 5. The numbers in these charts should be interpreted as: When I am in stage X, what is the expected effect on outcome Y? In general, a higher stage is related to greater reductions in GDP growth. Fatalities become substantial in stage 11, whilst countries in stage 12 suffer extremely intense violence.

Figure 5: Static effect of stages on outcomes

(a) Average GDP growth loss by stage, yearly

(b) Average number of fatalities by stage, monthly

However, viewing conflict as a static issue is like playing chess without thinking ahead. The charts in Figure 6 show the same outcomes but from a dynamic perspective i.e. we account for all possible futures for every stage. This answers the question: When I am in stage X, what is the expected effect on outcome Y in the future? Take stage 9 as an example, where in the static case we expect GDP to fall by only 0.2% and 0.1 fatalities per 1mn inhabitants. However, it is associated with significant future losses - GDP losses equivalent to 4x current GDP and 148 fatalities per 1mn inhabitants. Why? Because your future outlook contains a relatively high possibility of moving to stage 11 or 12 (and getting stuck in the conflict trap) compared to stages 1-4.

Figure 6: Dynamic effect of stages on outcomes

(a) Present value of future economic losses (relative to current GDP)

(b) Present value of future fatalities (per 1mn inhabitants)

Figure 6 is therefore a way to communicate the key point of the DEWAM: acting now to prevent future damages requires us to understand when these future damages are coming closer, even if they are not visible yet.

⁷ These associations are obtained via OLS regression analysis. We claim nothing causal about these relationships.

⁸ ODA is categorised as spend only relating to emergency response and peace/security.

Building block 4: Effect and costs of policies

At this point we have modelled the dynamics of conflict via the stages and their connection to measurable outcomes. The final step is to model policy interventions.

An intervention is defined via the transition matrix. Effective policies change the dynamics of conflict - they decrease the likelihood of moving to a higher stage (towards conflict) and increase the likelihood of moving to a lower stage (towards peace).⁹, ¹⁰ This is portrayed visually in Figure 7:

Figure 7: Change in probability of transitions under policy

Lastly, we need to associate interventions with a financial cost in each stage. This is challenging given the lack of available data on the monetary cost of different policies. Through close collaboration with policy-makers, we have derived cost estimates with two core assumptions:

• Fixed cost: Countries are assumed to be investing in policies to mitigate conflict, irrespective of what stage they are in. This is proportional to the size of the population.¹¹
• Variable cost: Costs are assumed to rise in line with the expected number of fatalities in each stage.¹² In other words, the more deaths resulting from a hypothetical conflict, the higher the intervention cost.

For context, policies in stage 4 interventions might relate to institution building at a cost of $145mn per month for a country with the population size of Nigeria. Stage 12 interventions would cost $10bn and would imply the mediation for a ceasefire, a massive deployment of peacekeeping troops and/or Disarmament, Demobilization and Reintegration (DDR) initiatives.¹³

⁹ The simulations test a range of policy effectiveness levels (2, 5, 10 and 25 per cent). The more effective a policy, the more probability mass is moved.

¹⁰ Keen observers may notice that the probability of staying in the same stage does not change uniformly across the stages. In the case that the total likelihood of moving to higher stages exceeds the total likelihood of moving to lower stages, the probability of staying where you are increases. The vice versa is also true.

¹¹ Expected spend of $0.25 per person.

¹² This requires making an assumption of how much costs rise for each additional fatality. As part of our simulations we test two values: $40,000 per fatality and $200,000 per fatality.

¹³ Intervention costs for Nigeria assume a variable cost assumption of $200,000 per fatality.

Results

Bringing all these aspects together allows us to simulate policy interventions. The results are reported as a benefit cost ratio (BCR) which can be interpreted as the dynamic long run return per $1 spent.^{14, 15} We also report uncertainty estimates in the form of standard deviations. A BCR less than 1 implies that the intervention is not cost effective.

Keep in mind that the BCR takes into account the imprecision of risk forecasts and the ineffectiveness of policies. This means that for low stages large benefits of prevention need to compensate for low escalation risks to bring the BCR over $1.

Our method not only takes into account imperfect forecasts but also optimal future policies into all futures. In the calculation of prevention we take into account what a rational policy-maker would do in a future in which the situation escalates.¹⁶ This might sound like a technical point but this ensures that the policy benefits are optimal, even under the assumption that the failure to prevent can be partially offset by later, optimal interventions.

Figure 8: Returns to interventions, Nigeria

(a) Including GDP growth effect

(b) Excluding GDP growth effect

Our model suggests that interventions in stage 9 are the most cost effective. When including/excluding the effects on GDP growth, interventions in this stage could deliver huge returns of approximately $300/$7 per dollar spent. Irrespective of the policy and cost assumptions, returns are markedly lower in stages 1-4 and 11-12 relative to 5-10. The intuition for this is as follows:

• Interventions in stable peace (stages 1-4): Interventions are relatively cheap, but potential gains are also low. Think of this as intervening in Sweden - the risk of escalation is so low that policies are not worthwhile. In these cases, the forecast precision is relatively low.
• The case for prevention (stages 5-10): Stages 5 to 10 represent a continuum of ‘preventative’ stages. Levels of violence are low, but elevated risks of escalation and the huge costs paid in the higher stages makes acting cost-effective. This is true even if it is not reacting to open violence, but merely follows an imprecise forecast.
• Interventions in conflict (stages 11-12): Armed conflict is severe in these stages leading to significant loss of life and economic growth, high displacement and a large increase in aid requirements. However, interventions have now become extremely costly - think of Afghanistan or Syria.

¹⁴ Please also make sure this text is gray rather than black.

¹⁵ Future gains/losses are discounted using a rate of 4%.

¹⁶ We use dynamic programming to conduct simulations. This simulates an infinite number of future months and undertakes a full dynamic optimisation with respect to policy.

Updated Prevention Gains

The below table shows, for 160+ countries worldwide, what risk stage they are in as at MM YYYY. We also show the returns to policy interventions in this stage across different scenarios:

• In the table below we always assume a policy effectiveness of 5%. This means that in any future situation, a country is 5% more likely to move towards more peaceful stages (and 5% less likely to move towards more perilous stages) than if it had not implemented the policy.
• We show results including and excluding the long-run effects of conflict on GDP growth. The scale of economic damages are so large that interventions always generate substantial returns when including GDP effects. Hence, we also present results that evaluate whether policy interventions can be cost-effective when only considering damages related to fatalities, displacement and ODA.
• We also differentiate between a low and high intervention cost scenario using two separate variable cost assumptions: $40k per fatality and $200k per fatality.

An important caveat is that the BCR's shown are conditional on making optimal policy decisions across all stages in the future. This is the essence of the dynamic nature of the model. The table orders countries according to the BCR without GDP and high violence costs of $200k per fatality to draw attention to relatively poor countries with high prevention gains.

Conclusion

We have devised a model that effectively integrates forecasts for evaluating returns to armed conflict prevention and de-escalation policies. This takes into account uncertainties faced by policy-makers including forecast precision, conflict dynamics, policy effectiveness and costs, whilst also capturing damages associated with conflict.

The core benefit of forecasts is that they permit actions to be taken in anticipation of crises. However, strong anticipation means acting on less precise forecasts. Taking action in low risk environments necessarily requires acting on false positives, i.e. cases where you make an intervention that in retrospect was not necessary. Our model demonstrates that there is a distinct cut-off at which these preventative actions become cost-effective i.e. the benefit of anticipation outweighs the cost of acting on false positives.

One limitation of our approach is that we do not model spatial spillovers. In other words, conflict and the implementation of policies in one country are assumed to have no effect on conflict or outcomes in other countries. We recognise this is a simplification, particularly for countries where there are extensive histories of conflict around borders. We seek to address this as part of our work on modelling policies at the subnational level.

Extension: Subnational policy interventions

Our work with policy-makers has highlighted that policies tend to be specific and localised due to the heterogeneity of conflict drivers and their subsequent outcomes. This motivated the development of a method that enables simulating policy interventions at a more fine-grained geographic unit - the grid cell level. They are a convenient and frequently used method for disaggregating the world map into uniform geographic units.¹⁷

Figure 9: Grid cell stage snapshot, Nigeria

(a) Grid cell stages, May 2005

(b) Grid cell stages, January 2023

The building blocks of the model are identical to those used for simulating national policies. However, some modifications are necessary to ensure simulations represent reality as closely as possible:

• Risk stages: We now have 8 stages and every grid cell is assigned a stage for every month.¹⁸ Stages 7 and 8 are the only situations in which violence occurs in a grid cell. Yet, they are differentiated by the amount of violence in directly neighbouring cells. Notice how in Figure 9b stage 8 appears in constellations (violent hotspots) whereas stage 7 tends to be more isolated (isolated outbreaks).
• Conflict dynamics: We explicitly model spatial spillovers. Levels of violence in one grid cell directly affect the transition likelihoods of neighbouring cells.
• Conflict damages: A lack of high-quality data makes accurately tracking outcomes (e.g. economic growth) at the grid cell level impossible. Instead we make a connection between levels of regional violence and measurable outcomes at the national level.¹⁹ In general, the higher the proportion of a country in more risky/violent stages, the worse the expected outcome as highlighted in Figures 9a and 9b.

We simulated potential gains over the next 12 months from a policy to de-escalate violence in Borno, Nigeria.²⁰ This serves to increase the likelihood of each grid cell in Borno transitioning to peace. In each month and for each grid cell, the intervention is assumed to be successful 25% of the time i.e. triggers movement to a lower stage. The rest of the country follows a stage trajectory unaffected by the policy, although a pacification of Borno has spillover effects to neighbouring regions. Our model suggests that this policy could save up to 400 lives and prevent $1.4bn in GDP losses between Jan 2023 and Jan 2024 in Nigeria.

Figure 10: Policy intervention in Borno, Nigeria

(a) Grid cells for policy intervention

(b) Indicative number of lives saved

This is a significant development from modeling national policy interventions. It enables evaluating policies which are actually taking place on the ground. Comparing and contrasting the value of different interventions is crucial, and our model can answer questions such as:

• Which regional parts of a country are vulnerable to escalation? What gains could we expect from preventing outbreaks in different regions?
• Is it more beneficial to de-escalate already violent hotspots, or act to prevent these hotspots spreading further?
• How can the timing and location of interventions around borders affect outcomes?

¹⁷ Each grid cell is approximately 55km x 55km.

¹⁸ The latest subnational model allocates stages for the period January 2005 to January 2023.

¹⁹ Specifically we use shares of population and GDP by grid cell. In this way we can compute the total share of a country’s population/economic activity that is in a given stage at a given point in time. OLS regressions are then used to associate these shares to measurable outcomes (GDP growth, fatalities, dis- placement and ODA) at the national level.

²⁰ Note that the methodology and results are still experimental. At present we do not assign costs to interventions in given sub-regions, hence results are presented as total gains rather than a benefit-cost ratio. The results shown assume a policy effectiveness of 25%.

Appendix

Four Models for Integrating Forecasting into Policymaking

Figure 11: FP21, Forecasting in Policymaking: Beyond Cassandra, Jan 2022

Our forecast usus millions of newspaper articles to make the conflict forecast. In our analysis of the content of the newspaper articles we rely on a so called topic model which summarizes the millions of articles and words into topics using unsupervised machine learning. The topic model allows us to calculate 15 topic shares for each country/month we display in the bubbles to the right.

The model assumes that if journalists write about a topic, say politics, they will use a different vocabulary than if they write about another topic, say conflict. The word “congress”, for example, is more likely to be used in an article about politics than in an article about conflict.

Our forecast method re-estimates the topic model every month and so the content of the topics changes across times.

Figure 12: Forecasting module topics, Sudan, April 2024

Figure 13: Example of topic-specific vocabulary, April 2024

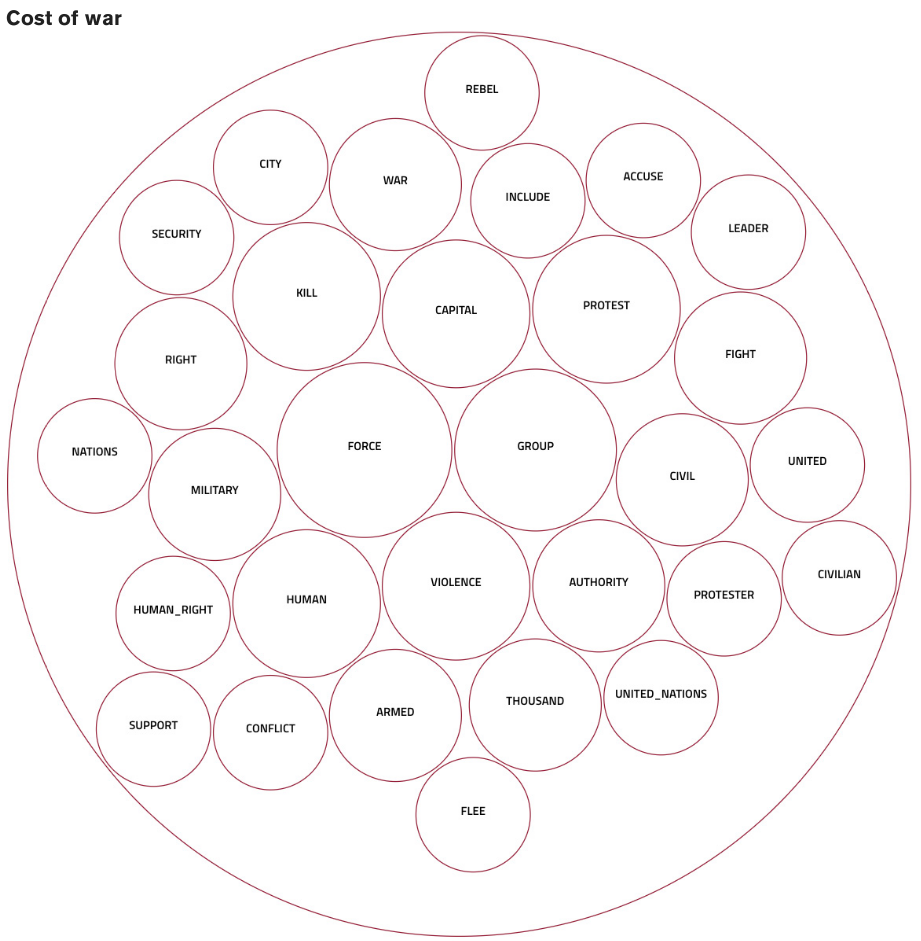
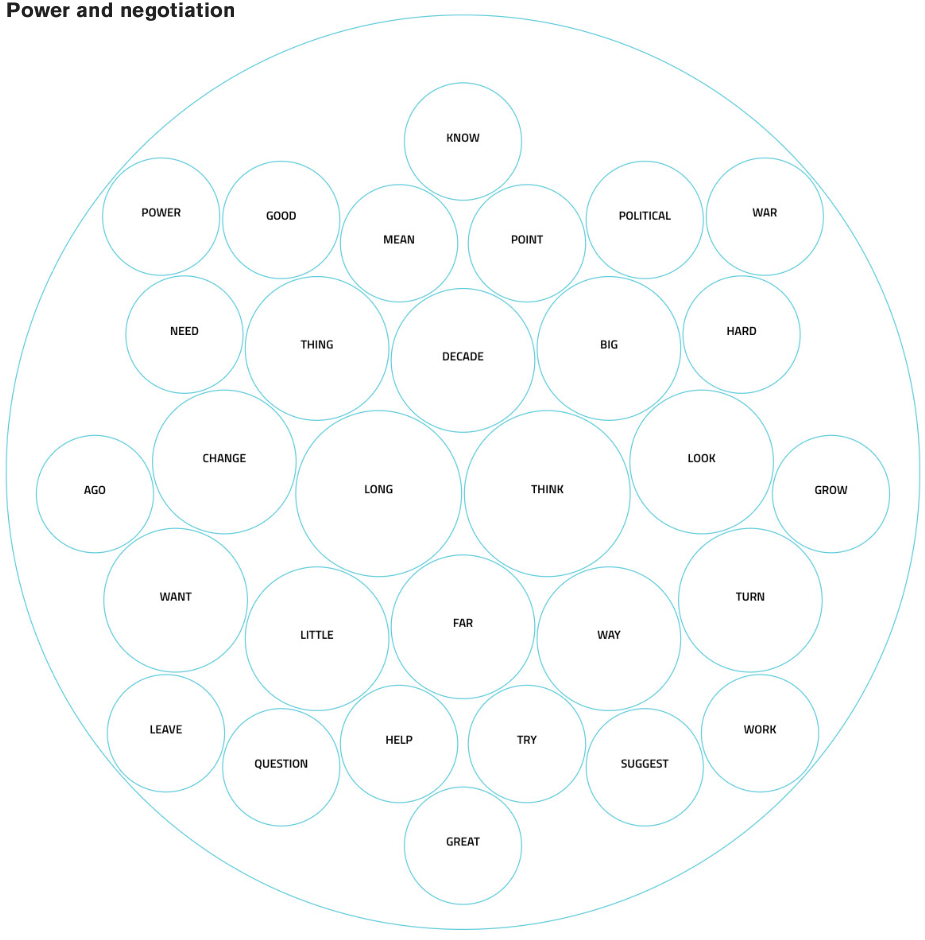
Figure 14: Uncertainty estimates for prevention gains, standard deviation